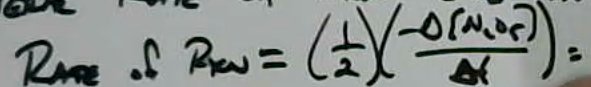Chapter 14

Chapter 14: Chemical Kinetics

Rates of reaction and the particulate nature of matter

• Kinetics:
  • Rates of reaction (speed)
  • The sequential steps of a reaction
• Affect the rates?
  • Concentration of the reactants
    • The more stuff that is present, the more collisions will occur and the rate of reaction will increase
  • Temperature of reaction
    • As the temperature increases, the rates also increase
  • Structure and orientation of particles
    • B-A + C → A-C + B
    • A-B + C -/->
      

Rates in a chemical reaction

• Rate = $\frac{\text{Concentration Change}}{\text{Time Change}}$
• 2 N2O5 → 4NO2 + O2
• Rate of formation for NO2: $\frac{\Delta [NO_2]}{\Delta t} = 3.7\times 10^{-5} M s^{-1}$
• Rate for formation for O2: $9.00\times 10 ^{-6} M s^{-1}$
• Rates must be positive
• General rate of reaction
  • Not formation or decomposition, but the rate of the entire reaction
  • Use stoichiometry to make sure that everything is equal to each other
  • Get one rate of reaction
    • Take each of the terms and divide it by the stoichiometry

    • 

• Instantaneous rate: rate of reaction at a single point in time
  • It is the slope tangent to the curve

The Rate Law

• How the reaction proceeds over the entirety of the reaction
• aA + bB → products
  • Rate Law: $\text{Rate} = k[A]^m[B]^n$
    • These exponents tell us how sensitive the reaction is to changes in concentration 
      
    • These exponents must be experimentally determined
      • This is because there are sequential steps for the reaction
    • The larger the exponent, the more sensitive it is to changes in concentration
• 3 common reaction orders that we can think about
  • We mean exponents by orders (m/n = 0, 1, 2)
    • Technically they can go higher or negative, but that is beyond the scope of General Chemistry II
  • If n = 0, the change in concentration has no effect on the rate
  • If n = 1, the rate is directly proportional to the concentration
  • If n = 2, the rate is proportional to the square of the concentration
    
• Overall reaction order: sum exponents
  • $\text{Rate} = k[A]^2[B]^1, \text{rate} = 3$

Determining the Order of a Reaction

• Initial rates: start of reaction
  • Change concentration and see the effect on the rate

The Integrated Rate Laws

First Order Integrated Rate Law

• $\text{Rate} = k[A]^1 = \frac{-\Delta [A]}{\Delta t}$
• $ln[A]_t = -kt + ln[A]_0$
  • $y=mx+b$ format

Second Order Integrated Rate Law

• $\text{Rate} = k[A]^2 = \frac{-\Delta [A]}{\Delta t}$
• $\frac{1}{[A]_t} = +kt + \frac{1}{[A]_0}$

Zeroth Order Integrated Rate Law

• $\text{Rate} = k[A]^0 = \frac{-\Delta [A]}{\Delta t}$
• $[A]_t = -kt + [A]_0$

The Half-Life of the Reaction

• The time needed for the concentration to be one half of its initial value
• First order: $ln[A]_t = -kt + ln[A]_0$
  • $ln(\frac{[A]_t}{[A]_0}) = -kt$
  • $[A]_t = \frac{1}{2}[A]_0$
  • $ln(\frac{\frac{1}{2}[A]_t}{[A]_0}) = -kt$
  • $-ln(2) = -kt_{\frac{1}{2}}$
  • $t_{\frac{1}{2}} = \frac{ln(2)}{k}$
  • For the first order reaction, $t_{\frac{1}{2}}$ has no concentration dependence
• Second order: $t_{\frac{1}{2}} = \frac{1}{k[A]_0}$
• Zeroth Order: $t_{\frac{1}{2}} = \frac{[A]_0}{2k}$

The Effect of Temperature on Reaction Rates

• The Arrhenius Equation
  • $k=Ae^{\frac{-Ea}{RT}}$
  • A is the frequency factor
  • -Ea is the activation energy
  • R is the gas law constant
  • T is the temperature in kelvin
• Activation energy
  • The amount of energy required to make the reaction go from products to reactants
• Change in energy is just final minus initial
• Frequency factor ($A$)
  • Number of times R approaches Ea barrier per unit of time
• Exponential factor ($\frac{-Ea}{RT}$)
  • Fraction of molecules with energy to get over the barrier
• Two-point form of the Arrhenius equation
  • $ln(A) = ln(k_1) + \frac{Ea}{R}(\frac{1}{T_1}) = ln(k_2) + \frac{Ea}{R}(\frac{1}{T_2})$
• The collision model (A)
  • Need 2 properly oriented molecules with sufficient energy to get over the barrier
  • Orientation factor
    • The reactants need to be oriented properly
  • Collision frequency (z)
    • Collision rate = $z[A][B]$
  • Reaction rate = orientation factor * collision rate * exponential factor

Reaction Mechanisms

• Series of molecular steps to get from reactants to products
  • Elementary steps
    • Individual molecular event
  • Reaction intermediate
    • Made in one step and consumer in another
      • Never seen in an equation
• Rates laws for elementary steps: molecularity
  • Unimolecular: one reactant (Rate = $k[O_3]$)
  • Bimolecular: two reactants (Rate = $k[O_3][O]$)
  • Termolecular: three reactants (exceedingly rare) (Rate = $k[O]^2[M]$)